A surprising way sigmoid function is applied in computer vision
Posted on Fri 30 November 2018 in Posts
Let's talk about all things image enhancement, what it is, why it is necessary and how do wavelets play a big part in it!
Introduction
Enhancement of images is an important preprocessing step in any image related system. Getting rid of noise, brightening, extraction of details - all of this helps in future steps, like feature extraction/engineering. There are many image enhancement techniques out there, let us look at one that uses a function which commonly is seen in neural networks
Sigmoid function
For all code below we will need matplotlib.pyplot, skimage and numpy. skimage is my preference of image processing library, I find it easy to understand and, if you want to modify something, you can always look under the hood of any function.
So, we will need
from matplotlib import pyplot as plt
%matplotlib inline
for plotting,
from skimage.data import astronaut
image = astronaut()
from skimage.util import img_as_float64 # make image in range [0..255], 8-bit integers
for image, image datatype adjustment and for some feature visualization, respectively.
Now, time for some visualization.
plt.figure(figsize=(10,9))
plt.imshow(image)
plt.axis('off');

Let's make sure we have our sigmoid function correctly defined:
def sigmoid(x):
return 1/(1+np.exp(-x))
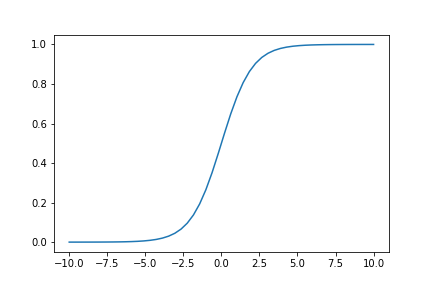
So, how do we use it to enhance the image? Well, let's look at the code:
image = astronaut()
image_ = np.zeros_like(image, dtype="float64")
def sigmoid(x):
return 1/(1+np.exp(-x))
def sigm_enh(I, alpha, beta):
I = img_as_float64(I)
I_out = I*sigmoid(alpha*(I-beta))#
return I_out
for i in range(3):
image_[...,i] = sigm_enh(image[...,i], 2, 50)#float(image.mean()))
fig, ax = plt.subplots(nrows=1, ncols = 2, figsize=(20,9))
ax[0].axis("off")
ax[0].imshow(astronaut())
ax[1].axis("off")
ax[1].imshow(rescale(image_,255))
and the result:


This is a simple way to bring image brightness up or down, especially comparing the results to some sort of metric (say, signal-to-noise ratio, or mean-squared error). In a different post, I will show a measure of image quality that our computer vision prof showed us (it's pretty cool, but has its own quirks).
We should try to do a little better/advanced with image enhancement. A function introduced in this paper dubbed "double sigmoid" looks something like this
\( \sigma_{double} = \mathrm{sign}(x-x_1) \exp \left(1- \frac{(x-x_1)^2}{s}\right)\)
And the plot of it
x = np.linspace(-10, 10, num=100)
plt.plot(x, double_sigmoid(x,0,2))
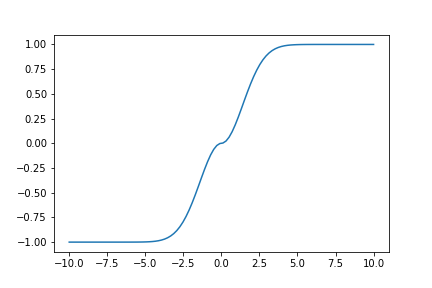
which is similar to two sigmoids complementing each other. Using the technique from the paper on a colored image, we need to be careful because this method is very sensitive to input parameters.
image = astronaut()
image_ = np.zeros_like(image, dtype="float64")
def double_sigmoid(x, x_1, s):
return np.sign(x - x_1) * (1 - np.exp(-((x - x_1) / s) ** 2))
def double_sigm_enh(I, x_1, k, s, b):
a = 1 / (double_sigmoid(k * (1 - b), x_1, s) - double_sigmoid(-k * (1 + b), x_1, s))
I_out = a * (double_sigmoid(k * (I - b), x_1, s) - double_sigmoid(-k * (I + b), x_1, s))
return I_out
for i in range(3):
image_[...,i] = double_sigm_enh(image[...,i].astype("float64"), k=0.9, b=0.0, x_1=0, s=100)
fig, ax = plt.subplots(nrows=1, ncols = 2, figsize=(20,9))
ax[0].axis("off")
ax[0].imshow(astronaut())
ax[1].axis("off")
ax[1].imshow(rescale(image_,255))
This can also be applied to grey-level images. The problem with this method of enhancement is that it heavily relies on a careful choice of parameters and is very sensitive to their values.
I really like that we can always find interesting applications of mathematical functions for image quality enhancement. In the next post I plan to talk about a measure that can be used to describe image quality.